Consideriamo il sottoinsieme S dei punti (X,Y,Z) di R³ soddisfacenti l’equazione -Z⁴+8Z³+X²+Y²-16Z²=0 . Che forma ha S ? Per capirlo prendiamo un punto (X,Y,Z) in S, allora:
-Z⁴+ 8Z³ + X² + Y² -16Z² =0. Tale condizione diventa:
X²+ Y² = Z⁴ -8Z³ + 16Z² = (Z² -4Z)² quindi posto v=Z, esiste u in [0,2pi) tale che:
X=(v² -4v)cosu
Y=(v²-4v)sinu.
da cui (X,Y,Z)=((v^²-4v)cosu,(v²-4v)sinu,v).
Viceversa se prendiamo una tripla ((v²-4v)cosu,(v²-4v)sinu,v), con v in R e u in [0,2pi) troviamo che:
-v⁴ + 8v³ + (v²-4v)² -16v =0. Pertanto:
S={ ((v²-4v)cosu,(v²-4v)sinu,u) , v∈R,u∈[0,2pi) }
Quindi il generico punto ((v²-4v)cosu,(v²-4v)sinu,u) di S può essere ottenuto per rotazione del punto (v²-4v,0,v) (che giace nel piano xz ) attorno all’asse z di un angolo u.
In pratica abbiamo scoperto che S è la superficie che si ottiene ruotando la curva:
A: v |—-> (v² -4v,0,v)
attorno all’asse z.
Per disegnare quindi S ci basta capire come è fatta la traccia di A. Questo non è difficile in quanto la traccia di A è proprio il grafico della funzione f(v)=v²-4v v∈ asse z. Quindi abbiamo ridotto l’esercizio a un puro studio di funzione. Si vede subito che il grafico di tale funzione è una parabola. Deduciamo che S è l’oggetto in figura:
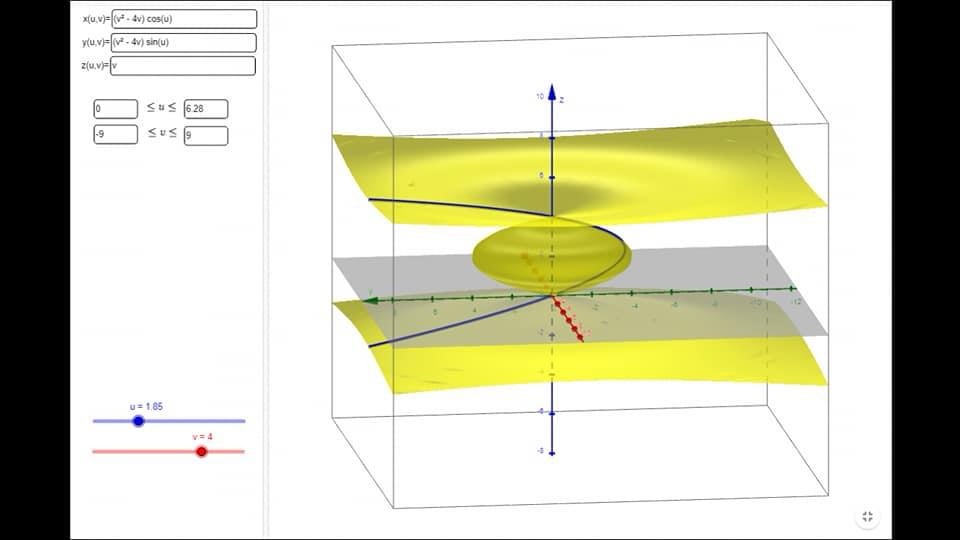
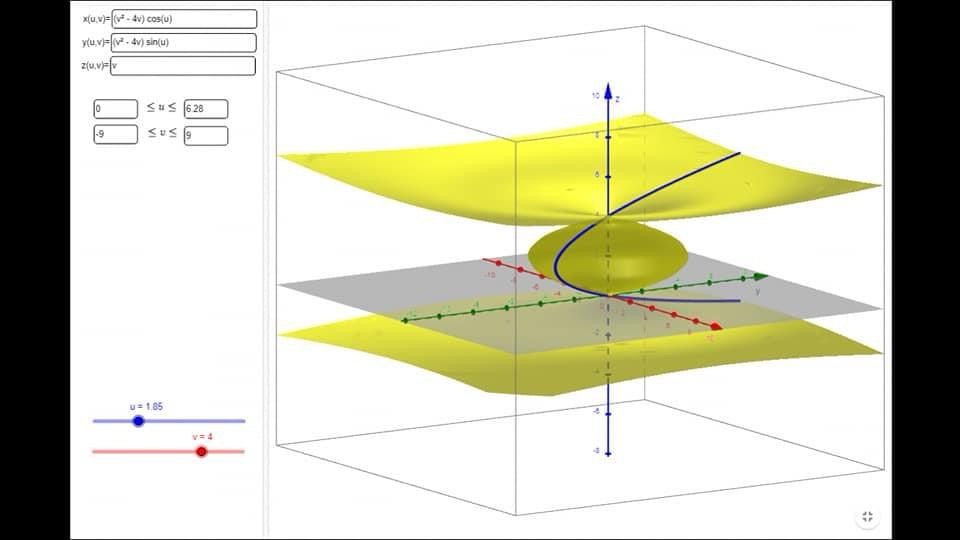
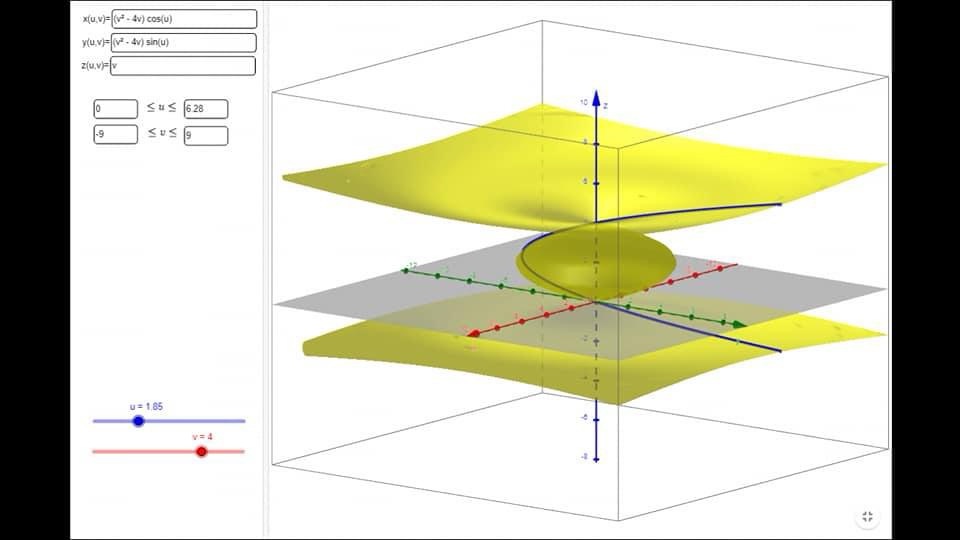

Leave a comment